YZOJ P1868 土地划分

时间限制：1000MS 内存限制：131072KB

难度：\(5.1\)

题目描述

在 \(Y\) 国有 \(N\) 座城市，并且有 \(M\) 条双向公路将这些城市连接起来，并且任意两个城市至少有一条路径可以互达。\(Y\) 国的国王去世之后，他的两个儿子 \(A\) 和 \(B\) 都想成为新的国王，但他们都想让这个国家更加安定，不会用武力解决问题。于是他们想将这个国家分成两个小国家 \(A\) 国和 \(B\) 国。现在，\(A\) 拥有 \(1\) 号城市，\(B\) 拥有 \(N\) 号城市，其他的城市还尚未确定归属哪边。

由于大家都想让国家变得更好，而某些城市的人民愿意国王的 \(A\) 儿子作为他们的领袖，而某些城市更看好 \(B\)，而为了交通的便捷，如果划分后的公路连接两个同一个国家的城市，那么更利于城市之间的交流。于是大臣们设计了一种对土地划分的评分机制，具体如下：

1，对于城市 \(i\) ，如果它划分给 \(A\) 国，将得到 \(VA[i]\) 的得分；划分给 \(B\) 国，将得到 \(VB[i]\) 的得分。

2，对于一条公路 \(i\) ，如果它连接两个 \(A\) 国的城市，将得到 \(EA[i]\) 的得分；连接两个 \(B\) 国的城市，将得到 \(EB[i]\) 的得分；否则，这条公路将失去意义，将扣除 \(EC[i]\) 的得分。

现请你找到最优的土地划分，使得这种它的评分最高。

输入格式

第一行包含两个整数 \(N\)，\(M\)，含义如问题描述所示。

接下来一行 \(N-2\) 个非负整数，表示 \(VA[2..N-1]\) 。

接下来一行 \(N-2\) 个非负整数，表示 \(VB[2..N-1]\) 。

接下来 \(M\) 行，每行五个非负整数描述一条公路：\(X, Y, EA[i], EB[i], EC[i]\)，含义如问题描述所示。

输出格式

输出一个整数，表示最高评分。

样例输入

3 3

1 2 2 6 2

2 3 8 5 7

1 3 9 4 1

样例输出

11

数据规模与约定

\(100\%\) 的数据 \(N \leq 10000, M \leq 40000\)；

保证运算过程中及最终结果不超过32位带符号整数类型的表示范围。

Source: BZOJ 3511

听说是贾教流的模板题？？？

传说中的论文：浅析一类最小割问题(pty).pdf

其实我不是很看得懂 QAQ（太菜

还有一种奇怪的做法：

\(S\) 向 \(1\) 连 \(\infty\) 的边，\(N\) 向 \(T\) 连 \(\infty\) 的边。

\(S\) 向 \(i\) 连 \(VA_i\) 的边，\(i\) 向 \(T\) 连 \(VB_i\) 的边。

对于原图中的一条边 \(i, \; x \leftrightarrow y\) ：新建一个点 \(NA\) ，\(S\) 向 \(NA\) 连 \(EA_i+EC_i\) 的边，\(NA\) 分别向 \(x, y\) 连 \(\infty\) 的边；再新建一个点 \(NB\) ，\(NB\) 向 \(T\) 连 \(EB_i+EC_i\) 的边，\(x, y\) 分别向 \(NB\) 连 \(\infty\) 的边。

跑最小割，取没有被割掉的边权（指权值中 \(VA,VB,EA,EB\) 的部分），最后加上 \(\sum {EC}\) 就是本题的答案。

假设原图中的点有 \(1,2,3,N\) ，边有 \(2 \leftrightarrow 3, 3 \leftrightarrow N\) ，那么建出来的图是这样的：

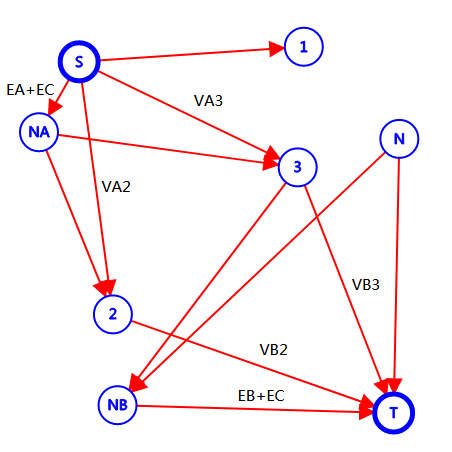
（注：图中未注明边权的为 \(\infty\)）

若同时割掉 \(VA_2, VB_3\)（或 \(VA_3, VB_2\)），那么有

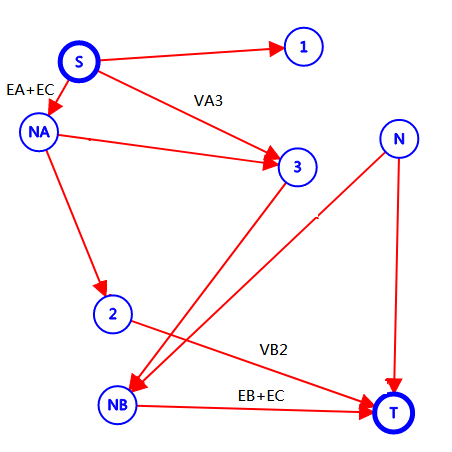
要使 \(S \rightarrow T\) 不连通，必须同时割掉 \(EA+EC, EB+EC\) ，对真正答案贡献了 \(VA_3+VB_2-EC\)（或 \(VA_2+VB_3-EC\)）。

若同时割掉 \(VA_2, VA_3\)，那么有

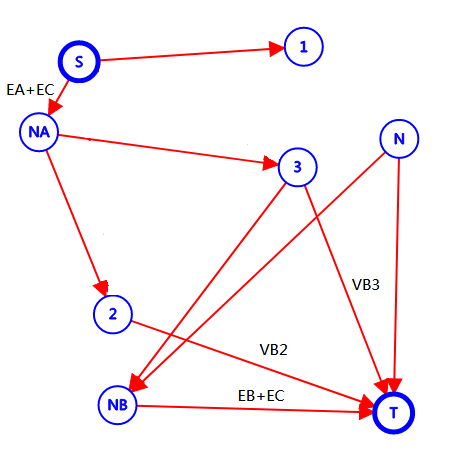
要使 \(S \rightarrow T\) 不连通，必须割掉 \(EA+EC\) ，对真正答案贡献了 \(VB_2+VB_3+EB\) 。

若同时割掉 \(VB_2, VB_3\)，那么有

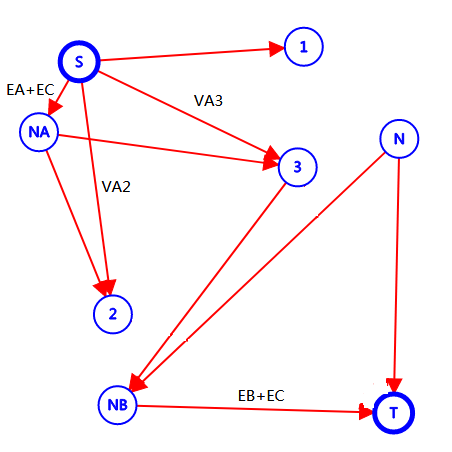
要使 \(S \rightarrow T\) 不连通，必须割掉 \(EB+EC\) ，对真正答案贡献了 \(VA_2+VA_3+EA\) 。

以此类推，可证其正确性。

~~就是点数变成 \(N+2M\) 有点慢而已。~~

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <climits>

#define INFINITE 0x7F7F7F7F
#define _min(_a_,_b_) ((_a_)<(_b_)?(_a_):(_b_))

inline int getnum()
{
	register char c=0;
	while(!(c>='0' && c<='9'))
		c=getchar();
	register int a=0;
	while(c>='0' && c<='9')
		a=a*10+c-'0',c=getchar();
	return a;
}

#define GetReverse(_x) ((_x)&1 ? (_x)+1 : (_x)-1)
int gcnt,ghead[105050],gnext[1505050],gnode[1505050],gflow[1505050];
inline void insertLine(register int s,register int t,const int&v)
{
	gnext[++gcnt]=ghead[s],ghead[s]=gcnt,gnode[gcnt]=t,gflow[gcnt]=v;
	gnext[++gcnt]=ghead[t],ghead[t]=gcnt,gnode[gcnt]=s,gflow[gcnt]=0;
}

int S,T;
int dist[105050];
inline bool BFS()
{
	static int lst[105050];
	register int front=0,rear=0;
	memset(dist,0,sizeof(dist));
	
	dist[S]=1,lst[rear++]=S;
	while(front<rear)
	{
		register int now=lst[front++];
		for(register int j=ghead[now],t;j;j=gnext[j])
			if(gflow[j]>0 && !dist[t=gnode[j]])
				dist[t]=dist[now]+1,lst[rear++]=t;
	}
	return dist[T];
}

int cur[105050];
int DFS(register int now,register int mxflow)
{
	if(now == T)
		return mxflow;
	
	for(register int j=cur[now],t;j;j=gnext[j])
	{
		cur[now]=j,t=gnode[j];
		if(!(gflow[j]>0 && dist[t]==dist[now]+1))
			continue;
		register int nf=DFS(t,_min(mxflow,gflow[j]));
		if(nf)
		{
			gflow[j]-=nf;
			gflow[GetReverse(j)]+=nf;
			return nf;
		}
	}
	
	return 0;
}

int main()
{
	register int N=getnum(),M=getnum();
	S=N+M+M+1,T=S+1;
	insertLine(S,1,INFINITE),insertLine(N,T,INFINITE);
	register int t,tS=0;
	for(register int i=2;i<=N-1;i++)
		insertLine(S,i,(tS+=(t=getnum()),t));
	for(register int i=2;i<=N-1;i++)
		insertLine(i,T,(tS+=(t=getnum()),t));
	register int tEC=0;
	for(register int i=1;i<=M;i++)
	{
		register int x=getnum(),y=getnum(),EA=getnum(),EB=getnum(),EC=getnum();
		tS+=EA+EB;
		tEC+=EC;
		register int NA=N+i,NB=N+M+i;
		insertLine(S,NA,EA+EC);
		insertLine(NA,x,INFINITE),insertLine(NA,y,INFINITE);
		insertLine(NB,T,EB+EC);
		insertLine(x,NB,INFINITE),insertLine(y,NB,INFINITE);
	}
	
	register int ans=0;
	while(BFS())
	{
		for(register int i=1;i<=T;i++)
			cur[i]=ghead[i];
		while(int nf=DFS(S,INFINITE))
			ans+=nf;
	}
	printf("%d\n",tS-(ans-tEC));
	
	return 0;
}

100

101

102

103

104

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <climits>

#define INFINITE 0x7F7F7F7F

#define _min(_a_,_b_) ((_a_)<(_b_)?(_a_):(_b_))

inline int getnum()

{

while(!(c>='0' && c<='9'))

c=getchar();

while(c>='0' && c<='9')

a=a*10+c-'0',c=getchar();

return a;

}

#define GetReverse(_x) ((_x)&1 ? (_x)+1 : (_x)-1)

int gcnt,ghead[105050],gnext[1505050],gnode[1505050],gflow[1505050];

inline void insertLine(register int s,register int t,const int&v)

{

gnext[++gcnt]=ghead[s],ghead[s]=gcnt,gnode[gcnt]=t,gflow[gcnt]=v;

gnext[++gcnt]=ghead[t],ghead[t]=gcnt,gnode[gcnt]=s,gflow[gcnt]=0;

}

int S,T;

int dist[105050];

inline bool BFS()

{

static int lst[105050];

memset(dist,0,sizeof(dist));

dist[S]=1,lst[rear++]=S;

while(front<rear)

{

for(register int j=ghead[now],t;j;j=gnext[j])

if(gflow[j]>0 && !dist[t=gnode[j]])

dist[t]=dist[now]+1,lst[rear++]=t;

}

return dist[T];

}

int cur[105050];

int DFS(register int now,register int mxflow)

{

if(now == T)

return mxflow;

for(register int j=cur[now],t;j;j=gnext[j])

{

cur[now]=j,t=gnode[j];

if(!(gflow[j]>0 && dist[t]==dist[now]+1))

continue;

if(nf)

{

gflow[j]-=nf;

gflow[GetReverse(j)]+=nf;

return nf;

}

return 0;

}

int main()

{

S=N+M+M+1,T=S+1;

insertLine(S,1,INFINITE),insertLine(N,T,INFINITE);

for(register int i=2;i<=N-1;i++)

insertLine(S,i,(tS+=(t=getnum()),t));

for(register int i=2;i<=N-1;i++)

insertLine(i,T,(tS+=(t=getnum()),t));

for(register int i=1;i<=M;i++)

{

tS+=EA+EB;

tEC+=EC;

insertLine(S,NA,EA+EC);

insertLine(NA,x,INFINITE),insertLine(NA,y,INFINITE);

insertLine(NB,T,EB+EC);

insertLine(x,NB,INFINITE),insertLine(y,NB,INFINITE);

}

while(BFS())

{

for(register int i=1;i<=T;i++)

cur[i]=ghead[i];

while(int nf=DFS(S,INFINITE))

ans+=nf;

}

printf("%d\n",tS-(ans-tEC));

return 0;

}

YZOJ P1868 土地划分

题目描述

输入格式

输出格式

样例输入

样例输出

数据规模与约定

发表回复 取消回复

发表回复取消回复