[研学] 质因数分解及素性判定
时间:2018.10 ~ 2019.3
参加成员:Modem_ Lagoon _Qijia mnihyc
感觉这个是人生巅峰了, Lagoon 上清华,剩下我们三也退役了,摆在这留作纪念ww 拿濑户口的话来说,就是萌新那会才是最辉煌的时期www
-
【序言】
质数的研究一直是数学与信息学领域中的重要课题,质数的判定与质因数分解在现代通讯保密领域中更是发挥着重要的作用,本课题小组将通过此次研学机会对不同规模下自然数素性判定及质因数分解的有效算法进行探究,加深对该领域的了解和理解。
-
【1.0】素数的定义
素数,又称质数。一个数 \(n\) 是素数当且仅当它是大于 \(1\) 的自然数且它的因数有且仅有 \(1\) 与 \(n\) 。
-
【1.1】记号与规定
-
- 记 \(\displaystyle\mathbb{R}\) 表示实数集,\(\displaystyle\mathbb{N}\) 表示自然数集,\(P\) 表示素数集。
- 勒让德符号 \(\displaystyle\left( {\frac{n}{p}} \right)\)。设 \(\displaystyle p \in P,n \in \mathbb{N}\)。
-
【1.2】素数的一些性质
- \(P\) 是无限集。
- 对于任意大于 \(1\) 的自然数,它要么是个素数,要么可以分解为若干素数之积,并且在忽略顺序的情况下,这样的分解是唯一的。
- 小于 \(n\) 的质数大约有 \(\ln n\) 个。
- 一个合数 \(n\) 最小的素因数因数一定小于 \(\sqrt n \)。
- 费马小定理:设 \(p\) 是大于 \(2\) 的素数,则对于任意正整数 \(n\) 均有 \(\displaystyle \begin{array}{*{20}{c}}{{n^{p – 1}} \equiv 1}&{(\bmod p)}\end{array}\)。
- Mertens’ second theorem。
-
【2.0】素性判定
因为素数集为无限集,并且素数的分布没有规律,所以我们需要实现一个算法来判定一个数是否为素数。而素性判定算法正是这样一类算法:输入一个整数,返回这个数是“素数”还是“合数”。
-
【2.1】暴力素性判定
-
【2.1.1】算法过程
-
-
-
- 输入数需要判断的数 \(n\)。
- 枚举所有大于 \(2\) 小于 \(\sqrt n \) 的整数 \(d\),判断 \(d\) 是否为 \(n\) 的因数。
- 若存在 \(d\) 是 \(n\) 的因数,则返回 \(0\);否则,返回 \(1\)。
-
-
-
【2.1.2】正确性证明
-
由定义可知,没有除了 \(1\) 与 \(n\) 以外因数的大于 \(1\) 的正整数 \(n\) 为素数,因此素性判定最朴素的方法便是枚举因数。上述算法的正确性基于以下结论:一个数合数最小的非 \(1\) 因数一定小于 \(\sqrt n \)。运用反证法,假设 \(n\) 的最小因数 \(d > \sqrt n \),那 \(\displaystyle \frac{n}{d}\) 为整数且 \(\displaystyle \frac{d}{n} < \sqrt n \),并且由于 \(\displaystyle n \div \frac{d}{n} = n\),因此 \(\displaystyle \frac{d}{n}\) 是比 \(d\) 小的 \(n\) 的因数,与 \(d\) 的最小性矛盾。故该结论成立。
-
-
【2.1.3】复杂度分析
-
显然时间 \(O(\sqrt n )\),空间 \(O(1)\)。
-
-
【2.1.4】代码实现
-
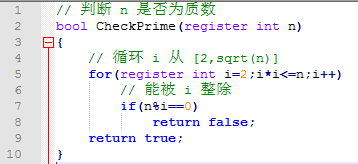
上述算法能通常能在合理的时间内实现单个数的素性判定,但当需要判定多个数的素性时往往需要“筛法”的帮助。
-
【2.2】埃式筛法
在数论算法中,枚举因数往往比枚举倍数困难许多。正难则反,既然素性判定难以快速实现,那么不如将目光投向合数,找出所有的合数,那么剩下的不就是质数了吗?筛法正基于这一思想。
-
-
【2.2.1】算法过程
-
-
-
- 输入 \(n\),表示要找出 \([2,n]\) 中的所有素数。
- 依次枚举 \([2,\sqrt n ]\) 中的数,如果 \(x\) 没有被筛掉,枚举 \([2,n]\) 范围内所有数 \(x\) 的倍数,记录为合数。
- \([2,n]\) 中剩下的所有数记录为质数。
- 算法结束,可在数表中查询 \(n\) 的素性。
-
-
-
【2.2.2】正确性证明
-
同样,本算法只用枚举 \([2,\sqrt n ]\) 中的数。
如果一个数 \(n\) 是合数,那么它一定存在一个小于 \(\sqrt n \) 的质因数 \(p\),\(p\) 一定在 \(n\) 之前被枚举到,并且将 \(n\) 记录为合数,因此剩下的数一定是素数。
-
-
【2.2.3】复杂度分析
-
时间复杂度 \(O(n\log \log n)\),空间复杂度 \(O(n)\)。
空间复杂度显然。埃式筛法的瓶颈复杂度在枚举每个质数的倍数上,也就是 。由Mertens’ second theorem,可知 (\(M\) 为Meissel–Mertens 常数),因此埃式筛法复杂度为 \(O(n\log \log n)\)。
-
-
【2.2.4】代码实现
-
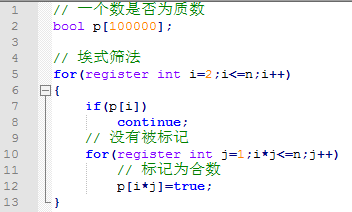
尽管 \(O(n\log \log n)\) 已经十分接近 \(O(n)\),但仍有优化的空间。欧拉筛法,又称线性筛法可在严格 \(O(n)\) 的时间内判定 \([2,n]\) 中所有数的素性。并且线性筛法还可以用于一些积性数论函数的求值。
-
【2.3】线性筛法
-
【2.3.1】算法过程
-
-
-
- 输入 \(n\),表示实现 \([2,n]\) 内的素性判定。
- 枚举从小到大 \([2,n]\) 的数,枚举到数 \(m\) 时,若其还未被标记,则将其加入素数集。对于所有枚举到的 \(m\),从小到大枚举素数集中所有满足 \(m \times p \le n\) 的素数 \(p\),将 \(m \times p\) 标记。一旦在枚举过程中出现 \(p|m\),则跳出素数的枚举。
-
-
-
- 算法结束,返回素数集与数表。
-
-
-
【2.3.2】正确性证明
-
线性筛法与埃式筛法的基本过程相同,关键在与“一旦在枚举过程中出现 \(p|m\),则跳出素数的枚举”这一步。这样做的正确性基于代数基本定理。因为我们是从小到大枚举素数的,这种弹出使得每个数会且只会被它的最小素因数筛掉。正是这种特性赋予了线筛递推处理积性函数值的能力。
-
-
【2.3.3】复杂度分析
-
因为每个数会且只会被它的最小素因子筛去一遍,所以时间复杂度显然就是 \(O(n)\)。空间也是 \(O(n)\)。
-
-
【2.3.4】代码实现
-
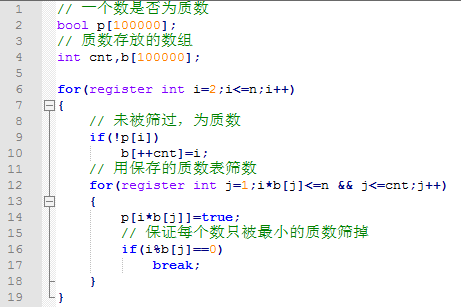
如果判定出范围内所有数的素性,那么线性筛法已经做到了时间与空间线性,无法再优化了。但是很多时候我们只需判定出几个大整数的素性,这时线性的复杂度就成了浪费。而 Miller-Rabin 素性测试就是一种针对单个数素性判定的优秀算法。
-
【2.4】Miller-Rabin素性测试
-
【2.4.0】前置理论与方法
-
【2.4.0.1】费马小定理
-
-
若 \(p\) 是一个质数,\(a\) 是一个不与 \(p\) 互质的正整数且 \(1 \le a < p\),那么 \(\displaystyle \begin{array}{*{20}{c}}{{a^{p – 1}} \equiv 1}&{(\bmod p)}\end{array}\) 。
-
-
-
【2.4.0.2】二次探测
-
-
如果对于质数 \(p\) 有正整数 \(x < p\),若 \(\displaystyle \begin{array}{*{20}{c}}{{x^2} \equiv 1}&{(\bmod p)}\end{array}\),那么 \(\displaystyle \begin{array}{*{20}{c}}{x = \pm 1}&{(\bmod p)}\end{array}\) 为此方程唯一的两个非平凡根。
-
-
【2.4.1】算法的过程与正确性
-
对于一个奇质数 \(n\),记 \(\displaystyle n – 1 = {2^k}d\) 且 \(2\not|d\) 。
若 \(a\not|d\),则易证有 \(\displaystyle \begin{array}{*{20}{c}}{{a^d} \equiv 1}&{(\bmod n)}\end{array}\) 或 \(\displaystyle \begin{array}{*{20}{c}}{{a^d}/{a^{2d}}/{a^{{2^2}d}}/ \cdots /{a^{{2^{k – 1}}d}} \equiv – 1}&{(\bmod n)}\end{array}\)。
对于一个质数 \(n\),由 Lemma.1 可得,\(\displaystyle \begin{array}{*{20}{c}}{{a^{{2^k}d}} \equiv {a^{n – 1}} \equiv 1}&{(\bmod n)}\end{array}\)。
又因为 \(\displaystyle {a^{{2^r}d}} = {({a^{{2^{r – 1}}d}})^2}\),同时由 Lemma.2 可知,\(\displaystyle \begin{array}{*{20}{c}}{{a^{{2^{r – 1}}d}} \equiv \pm 1}&{(\bmod n)}\end{array}\):
若 \(\displaystyle \begin{array}{*{20}{c}}{{a^{{2^{r – 1}}d}} \equiv – 1}&{(\bmod n)}\end{array}\),那么第二个条件成立;
若 \(\displaystyle \begin{array}{*{20}{c}}{{a^{{2^{r – 1}}d}} \equiv 1}&{(\bmod n)}\end{array}\),那么继续往下探测,直到得到 \(\displaystyle \begin{array}{*{20}{c}}{{a^d} \equiv 1}&{(\bmod n)}\end{array}\),那么就与第一个条件矛盾。
Miller-Rabin 的探测方法:若 \(\begin{array}{*{20}{c}}{{a^d}1}&{(\bmod n)}\end{array}\) 且 \(\begin{array}{*{20}{c}}{{a^{{2^r}d}} – 1}&{(\bmod n)}\end{array}\)(\(0 \le r < k\) ),那么 \(n\) 就一定不是质数。
一般来说,选择多个质数的底 \(a\) 可以极大的降低错误率,若使 \(k\) 表示探测的次数,那么错误率可以降低至大约 \(\displaystyle {4^{ – k}}\) 。
研究表明,\(n < 3,215,031,751\) 时,最少可以选择 \(2,3,5,7\);
\(n < 3,825,123,056,546,413,051\) 时,最少可以选择 \(2,3,5,7,11,13,17,19,23\) ;
\(n < 18,446,744,073,709,551,616\) 时,最少可以选择 \(2,3,5,7,11,13,17,19,23,29,31,37\) 。
-
-
【2.4.2】算法的复杂度
-
使用快速幂乘法,\(n\) 表示需要探测的数,\(k\) 表示探测的次数,时间复杂度为 \(O(k{\log ^2}n)\) 。
-
-
【2.4.3】算法实现代码
-
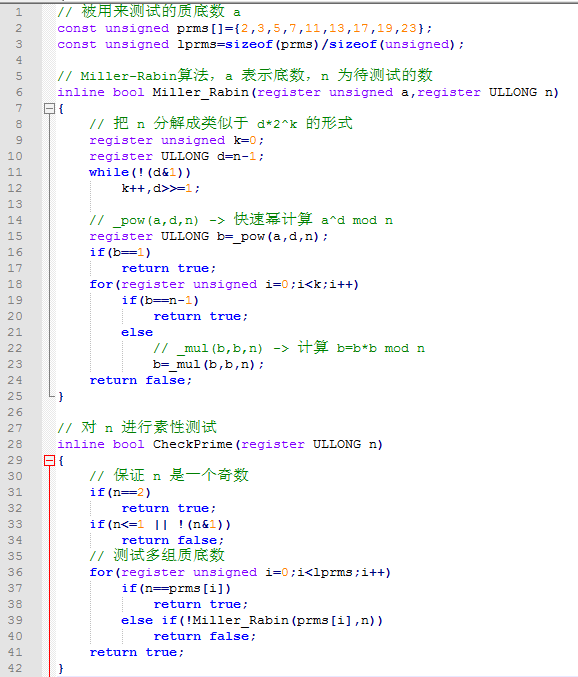
-
【3.0】质因数分解算法
在数论中,合数通常没有很好的性质。但由于代数基本定理成立,常常把合数分解为它的素因数。但素数分解并不容易实现,著名的RSA公钥加密算法就是利用两个大素数相乘容易,但对其乘积进行分解却极其困难的特点来实现加密的。质因数分解同样有着许多优秀算法。
-
【3.1】基于筛法的质因数分解
-
【3.1.1】算法流程
-
-
-
- 用筛法求出 \([2,\sqrt n ]\) 内的素数。
- 枚举每个小于当前的 \(\sqrt n \) 的素数,若 \(p\) 是 \(n\) 的因数,不断用 \(\displaystyle \frac{p}{n}\) 去更新 \(n\),直到 \(p\) 不再是 \(n\) 的因数,设这样一共做了 \(q\) 次,则将 \({p^q}\) 记入 \(n\) 的素因数分解式。
- 若枚举结束之后剩余的 \(n\) 大于 \(1\),将其加入素因数分解式。
- 算法结束,返回素因数分解式。
-
-
-
【3.1.2】正确性证明
-
因为枚举的都是质数 \(p\),而且不断用 \(\displaystyle \frac{p}{n}\) 更新 \(n\) 后,\(n\) 中已不再剩下该素因数。最后剩下的 \(n\) 若不为 \(1\),它也不含小于 \(\sqrt n \) 的素因数,由结论【1.2】,它也是一个素数。所以 \(n\) 中的每一个素因数都被完全分解出来,算法有正确性。
-
-
【3.1.3】复杂度分析
-
筛法时间复杂度 \(O(n)\),单次质因数分解时间复杂度 \(\displaystyle O({n^{\frac{1}{4}}})\);空间复杂度 \(O(n)\)。
-
-
【3.1.4】代码实现
-
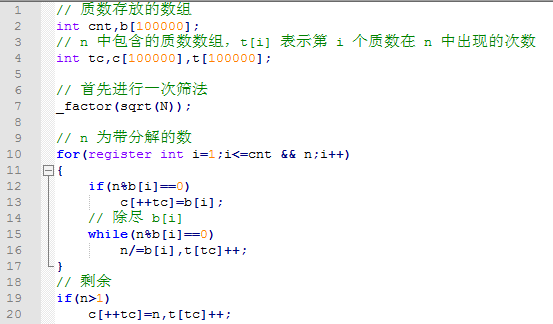
-
【3.2】Pollard-Rho算法
-
【3.2.1】算法思路与正确性证明
-
该算法用于找出一个数的质因数。该算法基于一个很普通的想法:随机一个数 \(a\),验证其是否是 \(n\) 的质因数。这个复杂度显然是错的。这时我们可以通过生日悖论来提高随机到因数的概率。生日悖论可抽象为:取 \(k\) 个 \([1,365]\) 间的整数,当 \(\displaystyle k \approx \sqrt {365} \) 时,\(k\) 个数中有两个数相同的概率已十分接近 \(\displaystyle \frac{1}{2}\)。所以,我们可以取 \(\sqrt n \) 个 \([1,n]\) 间的数,这样 \(k\) 个数中有两个数相减为 \(n\) 的因数的概率已十分接近 \(\displaystyle \frac{1}{2}\),提高了随机化的效率。
由于空间的限制,我们可以每次随两个数 \(p,q\),判断它们的差是否是 \(n\) 的因数。显然这个操作与上面不等价,但我们有一个很好的随机函数:
(\(\displaystyle \begin{array}{*{20}{c}}{f(x) = ({x^2} + c)}&{(\bmod n)}\end{array}\),\(c\) 为一个随机数)。
但这样可能进入循环。一个简易的判环方法叫做Floyd判环算法,大意为让另一个数 \(q\) 每次都执行两遍 \(f(q)\),当 \(q\) “追上” \(p\) 时及出现环。同时还有一个更为高效的判环算法——Brent的判环算法。即只有在循环了 \(2\) 的次幂时才移动 \(p\),同时把 \(q\) 设为移动前的 \(p\) ,判断时直接判断 \(p,q\) 是否相等。
-
-
【3.2.2】复杂度分析
-
这样可能一次找不出质因数,但我们可以多次改变 \(c\),直到找到为止。在这里要记得前面讲得生日悖论,因此这个过程期望不会重复很多次。
于是期望复杂度为 \(\displaystyle O({n^{\frac{1}{4}}})\)(包含 Miller-Rabin 判断素数及辗转相除求 \(\gcd\))。
-
-
【3.2.3】核心代码
-
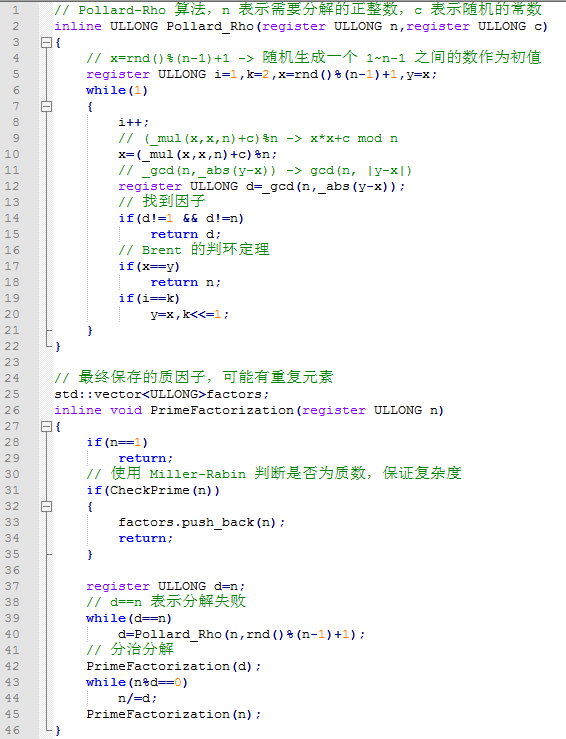
-
【3.3】二次筛法
二次筛法是一种基于费马分解的、运用构造技巧的极为强大的质因数分解算法,在其过程中需要实现高精度数的运算、Miller_Rabin、01高斯消元等子算法,可以称得上是质因数分解算法的集大成者。
-
-
【3.3.1】算法过程
-
由于算法过程的复杂性,这里将一些子算法的过程直接封装。
-
-
- 构造出一组素数基底 \(S\),其中每一个素数 \(p\) 都要满足 \(\displaystyle \left( {\frac{{n\bmod p}}{p}} \right) = 1\)(\(n\) 对 \(p\) 的勒让德符号)。
- 选择若干个 \({x_i}\),计算出一系列 \(\displaystyle Q({x_i}) = {({x_i} + \left\lfloor {\sqrt n } \right\rfloor )^2} – n\) 的值组成集合 \(T\)。
- 运用基于筛法的素因数分解方法,找出 \(T\) 中所有素因数集合 \(s\) 是 \(S\) 子集的 \(\displaystyle Q({x_i})\) 组成集合 \(B\)。
- 以 \(B\) 为基底使用01高斯消元构造出一组 \(j\) 使得 \(\displaystyle \Pi Q({x_j})\) 为平方数。
- 于是我们有 \(\displaystyle \Pi Q({x_j}) \equiv \Pi {({x_j} + \sqrt n )^2}(\bmod n)\),用费马分解法找出 \(n\) 的一个因数,如果是非平凡因子,递归求解,否则扩大 \(\displaystyle {{\rm{x}}_i}\) 范围重新计算。
- 若当前 \(n\) 为质数,直接返回;
-
-
-
【3.3.2】正确性证明
-
首先是费马分解法:
这种因数分解法是由费马提出并证明的。尝试找到 \(x,y\) 满足 \(\displaystyle \begin{array}{*{20}{c}}{{x^2} \equiv {y^2}}&{(\bmod n)}\end{array}\) ,这样就有 \(\displaystyle \begin{array}{*{20}{c}}{(x + y)(x – y) \equiv 0}&{(\bmod n)}\end{array}\),故 \(\displaystyle \gcd (x + y,x – y)\) 一定是 \(n\) 的因数,且大概率是非平凡因子。
然后是 \(Q(x)\) 的构造:
基于费马分解法,我们构造 \(\displaystyle Q(x) = {(x + \left\lfloor {\sqrt n } \right\rfloor )^2} – n\),这样只要找到 \(x\) 使 \(Q(x)\) 为完全平方数,就有 \(\displaystyle \begin{array}{*{20}{c}}{Q(x) = {{(x + \left\lfloor {\sqrt n } \right\rfloor )}^2}}&{(\bmod n)}\end{array}\) 而完全平方数说白了就是所有素因数个数都是偶数的数。但直接构造出这样的数并不容易,可以先选择一个素数集 \(S\),找出若干可以被 \(S\) 内数完全分解的 \(Q({x_i})\)。虽然单个 \(Q({x_i})\) 的每个素因数的个数可能不是偶数,但通过将 \(Q({x_i})\) 相乘最终就有能力将其补成偶数。而这时就可以列一个模 \(2\) 意义下的01线性方程组,求解出每个 \(Q({x_i})\) 对应的系数即可。
这样就兼顾了正确率与复杂度。
-
-
【3.3.3】时间复杂度
-
时间复杂度 \(\displaystyle {\rm{O}}({e^{\sqrt {\ln n\ln \ln n} }})\),空间复杂度 \(O(n)\)
证明较为繁琐,此处略去
-
【尾声】
以上的种种算法都可以帮助我们实现素数判定或完成质因数分解,他们对应着不同的时间与空间规模,因此在真正使用时要注意算法的选择。
有人说,数论是数学王冠上的璀璨明珠,而素数有是数论中不可或缺的一个部分。人类关于素数的研究永远不会停歇,素性判定与质因数分解的算法也是这样。上文中提到的二次筛法已经是质因数分解中的优秀算法,而在2002年,AKS素性测试也成为了首个确定性的高效素性判定算法。而1994年秀尔算法的出现,也给了我们一个美好的展望——量子计算机能在对数时间内真正高效地解决质因数分解问题。
相信在未来,随着硬件与软件的进步,也将会有更多优秀的算法涌现,让素数在信息时代绽放更加灿烂的光彩。
Orz mnihyc Orz