YZOJ P1310 [省队训练][NOI模拟7]车的放置
时间限制:1000MS 内存限制:262144KB
难度:\(8.0\)
-
题目描述
有 \(N\) 个 \(1 \times h[i]\) 的矩形小棋盘,底边边长为 \(1\),在一条直线上拼成了一个畸形的棋盘。
高度 \(h[i]\) 给出,第 \(i\) 个矩形的高为 \(h[i]\),例如 \(h = [3, 2, 4, 2]\) 的图形如下: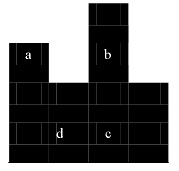
若两个车相互攻击仅当它们在同一列,或在同一行且在这一行它们之间棋盘格子都是存在的,例如上图中 \(a\) 与 \(b\) 是相互不攻击的,\(c\) 与 \(d\),\(b\) 与 \(c\) 均为相互攻击的。
现在要在这棋盘上放置恰好 \(K\) 个相互不攻击的车,问有多少种方案。
-
输入格式
输入第 \(1\) 行包括两个正整数 \(N\),\(K\),表示了棋盘的列数和放的车数。
第 \(2\) 行包含 \(N\) 个正整数,表示了棋盘每列的高度。
-
输出格式
输出包括一个非负整数,表示有多少种放置的方案,输出答案 \(\mod 1000000007\) 后的结果即可。
-
样例输入
|
1 2 |
5 2 2 3 1 2 4 |
-
样例输出
|
1 |
43 |
-
数据规模与约定
对于 \(100\%\) 的数据,有 \(N \leq 500\),\(K \leq 500\),\(h[i] \leq 1000000\) 。
把笛卡尔树建出来,在上面树形DP。
为了方便,在这里认为 笛卡尔树中的一个点 \(i\) 表示的矩形 不包括它的所有子节点所表示的矩形,即这个矩形的宽为 \(W=size_i\) ,高为 \(H=h_{i}-h_{father}\) 。
设 \(f_{i, j}\) 表示以 \(i\) 为根的子树中放 \(j\) 个车的方案数;\(t_{i, j}\) 表示以 \(i\) 为根的子树中放 \(j\) 个车,并且这 \(j\) 个车都不在 \(i\) 表示的矩形中 的方案数。
那么有 \(t_{i, j} = \sum\limits_{k=0}^{j}{f_{lson, k} \times f_{rson, j-k}}\) 。
还有 \(f_{i, j} = \sum\limits_{k=0}^{j}{ t_{j-k} \times C_{H}^{k} \times C_{W-\left(j-k\right)}^{k} \times k!}\) 。
初始值 \(f_{0, 0}=1\)
时间复杂度 \(O(nk^2)\)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
#include <cstdio> #include <cstdlib> #include <cstring> #include <climits> #define _min(_a_,_b_) ((_a_)<(_b_)?(_a_):(_b_)) #define _max(_a_,_b_) ((_a_)>(_b_)?(_a_):(_b_)) #define MOD 1000000007 inline int _pow(register int base,register int b) { register int ans=1; while(b) { if(b&1) ans=(long long)ans*base%MOD; base=(long long)base*base%MOD; b>>=1; } return ans; } int N,K,mh,h[505]; int fac[1050505],invfac[1050505]; #define _comb(_a_,_b_) (((_a_)>(_b_) ? 0 : (long long)fac[_b_]*invfac[_a_]%MOD*invfac[(_b_)-(_a_)]%MOD)) int lson[505],rson[505],size[505]; inline void PushUp(register int o) { size[o]=size[lson[o]]+size[rson[o]]+1; } int f[505][505]; void DFS(register int o,register int fa) { if(lson[o]) DFS(lson[o],o); if(rson[o]) DFS(rson[o],o); static int tf[505]; memset(tf,0,sizeof(tf)); for(register int j=0;j<=_min(size[o],K);j++) for(register int k=0;k<=j;k++) (tf[j]+=(long long) f[lson[o]][k] * f[rson[o]][j-k] %MOD)%=MOD; for(register int j=0;j<=_min(size[o],K);j++) for(register int k=0;k<=j;k++) (f[o][j]+=(long long) tf[j-k] * fac[k] %MOD* _comb(k,h[o]-h[fa]) %MOD* _comb(k,size[o]-(j-k)) %MOD)%=MOD; } int main() { scanf("%d%d",&N,&K); for(register int i=1;i<=N;i++) scanf("%d",&h[i]),mh=_max(mh,h[i]); invfac[0]=fac[0]=1; for(register int i=1;i<=mh;i++) fac[i]=(long long)fac[i-1]*i%MOD; invfac[mh]=_pow(fac[mh],MOD-2); for(register int i=mh-1;i>=1;i--) invfac[i]=(long long)invfac[i+1]*(i+1)%MOD; static int stk[505]; register int top=0; for(register int i=1;i<=N;i++) { register int last=0; while(top && h[stk[top]] > h[i]) PushUp(stk[top]),last=stk[top],stk[top--]=0; if(top) rson[stk[top]]=i; lson[i]=last,stk[++top]=i; } while(top) PushUp(stk[top--]); register int root=stk[1]; f[0][0]=1,DFS(root,0); printf("%d\n",f[root][K]); return 0; } |