YZOJ P3129 [校内训练20170627]跳格子

时间限制：1000MS 内存限制：524288KB

难度：$7.0$

• 题目描述

在一个花园里有一排 $n$ 个格子，这些格子编号为 $1$ 到 $n$ 。袋鼠喜欢在花园的格子上跳跃。

袋鼠的跳跃方式是这样的：一开始，袋鼠位于 $s$ 号格子上，接着它会选择一个尚未经过的格子上跳跃，经过 $n-1$ 次跳跃后，所有格子都被经过了一次，袋鼠的跳跃将结束。袋鼠总是会在 $t$ 号格子结束跳跃。

由于袋鼠中了病毒，所以如果上一步往前跳，那么这一步必须往后跳；反之，若上一步往后跳，那么这一步往前跳。

请问袋鼠有多少种跳跃的方案呢？

形式化地，你需要求出有多少个 $1$ 到 $n$ 的排列 $p_1, p_2, \cdots, p_n$，满足：

1， $p_1=s ，p_n=t$；

2， 对任意 $2 \leq i \leq n-1$，或者 $(p_i-1<p_i) \land (p_i+1<p_i)$ ，或者 $(p_i-1>p_i) \land (p_i+1>p_i)$ 。

• 输入格式

输入共一行，包含三个正整数 $n, s, t$ 。

• 输出格式

输出共一行，包含一个整数，表示跳跃的方案数对 $1,000,000,007$ 取模的结果。

• 样例输入【包含两组样例】

• 样例输出

• 样例 1 说明

从 $2$ 号格子到 $3$ 号格子的跳跃方案有两种，一种是 $2,1,4,3$，一种是 $2,4,1,3$ 。

• 数据规模与约定

 

 

 

---

 

 

 

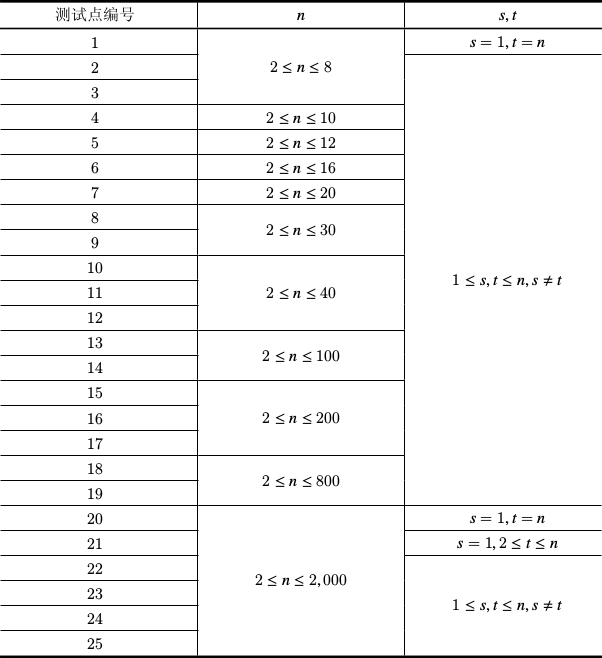
考场上疯狂打表找规律，然后还没找出来，调试代码没删，所以就爆了零。

听说本题有数学解，但是我太菜我不会我想不出来，这里是Wiki 的说明。

 

本题运用 接头DP 的方法统计方案数（接头DP？？？我也是第一次听说），即在DP的时候考虑当前格子和它的上一个及下一个格子（若存在）的连接情况。

记 o- 表示 从这个格子出发向右 或者 从右边到达这个格子结束，-o 表示 从这个格子出发向左 或者 从左边到达这个格子结束；>o 表示 从左边进入这个格子再从左边出去，o< 表示 从右边进入这个格子再从右边出去。（注意，由于题目的特殊限制，所以只有这四种情况）

那么对于第一个格子，因为它左边已经没有格子，所以它的接头只有两种情况。

1， 若 $(s = 1) \lor (t = 1)$ ，那么它只可能是 o- 这种情况。

2， 若 $(s \ne 1) \land (t \ne 1)$ ，那么它只可能是 o< 这种情况。

同样，对于第 $n$ 个格子，它右边已经没有格子，所以它的接头也只有两种情况。

1， 若 $(s = n) \lor (t = n)$ ，那么它只可能是 -o 这种情况。

2， 若 $(s \ne n) \land (t \ne n)$ ，那么它只可能是 >o 这种情况。

那么对于其他的非 $1$ 非 $n$ 的格子 $i$，它的接头也会有两种情况。

1，若 $(i = s) \lor (i = t)$，那么它可能为 o- 或 -o 的其中一种情况。

2，若 $(i \ne s) \land (i \ne t)$，那么它可能为 >o 或 o< 的其中一种情况。

例如样例 $1$ 对应 o< -o o- >o 和 o< o- -o >o 这两种连接情况。

注意到，连接的方向可能相同，但是连接的顺序可能不同，就如同上面的第 $1$ 个格子，所以状态只有一维是不够的。

因此，设 $f_{i, j}$ 为表示当前按顺序做到第 $i$ 个格子，此时剩余的未配对的 o< 形连接还有 $j$ 个的方案数。

考虑初始值，其实已经在上面有所涉及，即 $(s = 1) \lor (t = 1)$ 时 $f_{1, 0}=1$ ，$(s \ne 1) \land (t \ne 1)$ 时 $f_{1, 1}=1$ 。

考虑转移，假设当前做到第 $i$ 个格子，同样有两种情况。

1，$(i = s) \lor (i = t)$ ，可能为 o- 或 -o 。若是 o- ，则它对未配对的 o< 形连接的个数没有影响；若是 -o ，则它需要选择前面的一个未配对的 o< 进行接头配对。即 $f_{i, j}=f_{i-1, j}+\left( j+1 \right) \cdot f_{i-1, j+1}$ 。

2，$(i \ne s) \land (i \ne t)$，可能为 >o 或 o< 。若是 >o，则它可以选择之前任意两个未配对的 o< 并把它们连在一起，或者是连接从 $s$ 或 $t$ 出来的一条链（注意，仅当 $i>s$ 或 $i>t$ 时才能进行连接）；若是 o<，则它仅仅只是增加了一个未配对的 o< 。即 $f_{i, j}=f_{i-1, j-1}+j(j+1) \cdot f_{i-1, j+1} + [i>s]f_{i-1, j+1}+[i>t]f_{i-1, j+1}$ ，化简得 $f_{i, j}=f_{i-1, j-1}+(j+1)(j+[i>s]+[i>t]) \cdot f_{i-1, j+1}$ 。

由于全部做完一定不会剩下未配对的 o< 形连接，而不论是哪种情况一定不改变未配对的 o< 形连接的数量，答案即为 $f_{n, 0}=f_{n-1, 0}$ 。

这样的时间复杂度为 $O(n^2)$ 。