浅谈斜率优化——截距优化
最近(两个月前)学习了斜率优化 —— 一种优化 1D1D 动态规划转移方程的高效方法,在较高难度的比赛中是一种十分常见的 DP 优化手段。鉴于我之前(一年前)也稍微接触过一点相关方面的知识,但是完全没有搞懂(太菜了),最近(两个月前)再配合 orzCJK学长 提出的截距优化的思想理念才对于斜率优化问题有了深刻的见解,故在这里对 orzCJK学长 的 斜率优化_截距优化!.pdf 进行详细的解释说明。
首先,1D1D 指的是状态数 \(O(n)\) 转移 \(O(n)\) 的动态规划方程。在满足一些条件的情况下,斜率优化可以将转移的 \(O(n)\) 优化至 \(O(logn)\) 甚至可以到 \(O(1)\) 。这样时间复杂度就由 \(O(n^2)\) 变为 \(O(nlogn)\) 甚至是 \(O(n)\) ,可见斜率优化的高效性。
如果有一个 DP 方程的某个状态为 \(f_i\) ,如果能推导出类似于 \(f_i=c_i + \min\limits_{j<i \land \cdots}{\{a_j + w_i \cdot b_j\}}\) ,那么这个转移方程就可以使用斜率优化进行优化。
然而普通的转移方程并没有什么特殊的地方,使用经典的方法(我也不会)略显繁琐,所以现在我们要赋予它以几何意义。(时刻注意,这个转移方程的意义是对于一个 \(i\) 在 \(j < i\) 范围内寻找 \(j\) 使 \(a_j + w_i \cdot b_j\))最小。)
换一下变量名,设 \(y_j=a_j, k_i=-w_i, x_j=b_j\) ,那么这样需要最小化的式子就变为 \(\underbrace{a_j}_{y_j} – \underbrace{-w_i}_{k_i} \cdot \underbrace{b_j}_{x_j}\) 。这不就是截距 \(b = y – kx\) 吗?!!也就是说,要最小化的就是一条过 \(\left(x_j, y_j\right)\) 且斜率为 \(k_i\) 的直线的截距!
换句话说,把所有对于当前 \(i\) 可转移的 \(j\) 都表示为二维平面上的一个点 \(p_j=\left(x_j, y_j\right)\) ,我们需要做的就是在所有这样的点中,找到一个点,使经过它且斜率为 \(k_i\) 的直线的截距最小!这也是为什么斜率优化就是截距优化的原因,它其实优化的是截距!
现在想象一条斜率固定的直线从下往上平移,当它第一次经过某个点 \(p_j\) 时,这时的截距肯定取到最小值。那么这个点 \(p_j\) 在什么地方呢?显然,它会在所有 \(p\) 组成的下凸壳上。
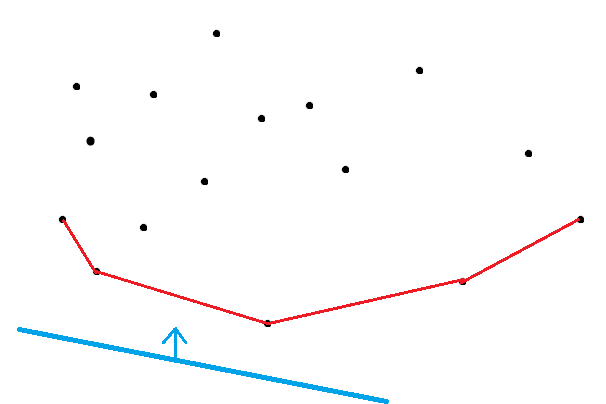
那么现在只要维护这个下凸壳,每次在上面找点使得截距最小,拿来更新 \(f_i\) 后把 \((x_i, y_i)\) 也加入下凸壳即可。
在这里,维护这个凸壳的情况分为三种:
-
1,\(x_j\) 和 \(k_i\) 均单调
这是最简单的情况。维护凸壳无非就是维护两个操作——查询和加入。
首先考虑如何找到最优的点使斜率固定且经过它的直线的截距最小。因为询问的斜率 \(k_i\) 是单调的(在这里假设它单调递增),所以每次找的点不可能在上一次找的点的左侧,这是因为下凸壳上两点之间的斜率也是单增的,查询的斜率增大意味着最优点只可能向右移动。
所以可以得到一种处理方法,如果队头的前两个点连成的直线的斜率 比 当前查询的斜率 \(k_i\) 还小,那么队头的那个点肯定是取不到了(如下图),因为这条直线会在到达第一个点之前先到达第二个点,所以弹出队头元素直到满足条件,这样就可以放心的取队头元素作为最优点贡献给 \(i\) 。
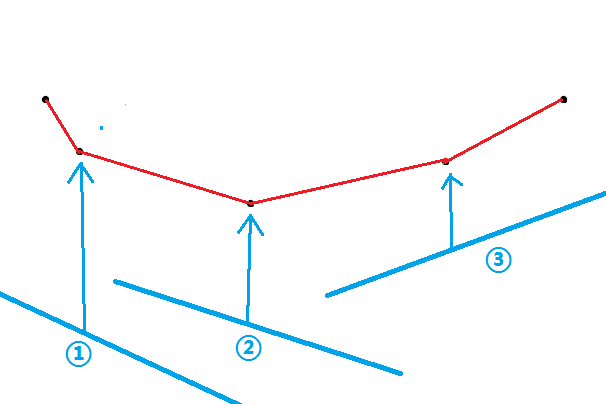
同理,因为加入的点的 \(x_j\) 也是单调的(在这里假设它单调递增),所以如果队尾两个点连成的直线的斜率 比 最后一个点和当前需要加入的点连成的的直线的斜率还大,说明图形凹进去了(如下图),由于维护的是下凸壳,所以需要把队尾元素弹出直到满足条件,最后再把当前点加入。
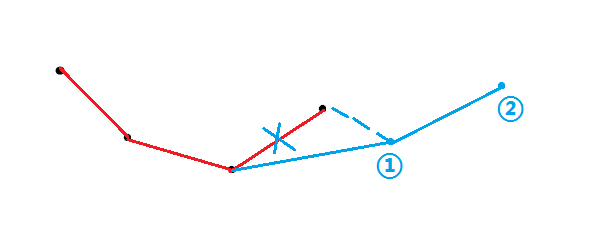
这样维护这个单调队列就是 \(O(n)\) 的,总时间复杂度 \(O(n)\) 。
-
2,只有 \(x_j\) 单调
\(x_j\) 是单调的,意味着仍然可以按照上面的方法加入一个点。那么查询呢?查询的 \(k_i\) 不是单调的,这就意味着不能像之前一样弹出队头元素来找到最优点,因为最优点失去了一个性质——只会单调移动。(即这次的最优点可能在上一个最优点的左边。)
重新考虑如何找到这个最优点。
注意到维护的下凸壳上所有直线的斜率都是单调递增的。设此时这条直线的斜率为 \(k\) ,最优点为 \(p_j\), \(p_j\) 到凸壳的上一个点的直线的斜率为 \(k_1\) ,\(p_j\) 到凸壳的下一个点的直线的斜率为 \(k_2\) ,那么 \(k \in [k_1, k_2]\) (如下图)。所以可以在凸壳上二分斜率,找到比当前斜率大的直线中斜率最小的直线,用它的左端点来贡献答案。
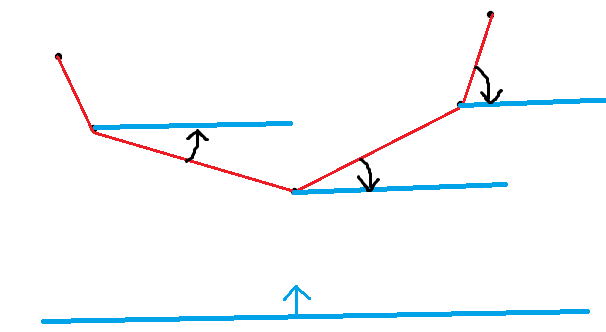
这样加入点仍是 \(O(1)\) ,查询就变成 \(O(logn)\) 了,总时间复杂度 \(O(nlogn)\) 。
-
3,\(x_j\) 和 \(k_i\) 都不单调
查询的 \(k_i\) 不单调还可以二分多个 \(O(log)\) 好说,但是这加入的 \(x_j\) 都不单调了,看起来似乎维护这个凸壳的复杂度就上去了。哦豁,完蛋,要写 Splay 维护下凸壳了。其实并不然,这个时候只需要用到一种神奇的分治算法 —— CDQ分治。
回顾一下上面斜率优化的写法:把可以实现把一个点加入单调队列的操作是因为加入的 \(x_j\) 是单调的,可以取队头元素为最小值是因为询问的斜率 \(k_i\) 是单调的。CDQ分治就是牢牢抓住这两点进行操作的。
因为是分治,所以要有一个分治区间 \([l, r]\) 表示用 \([l, mid]\) 中所有点的信息去更新 \((mid, r]\) 的最小值(可以神奇地证明这样做可以不遗漏更新所有的情况)。那么如何快速做到这个更新操作呢???很简单,只需要把 \([l, mid]\) 中的点按照 \(x\) 排序,\((mid, r]\) 中的元素按照斜率 \(k\) 排序,这样就可以按照上面的斜率优化的写法维护一个单调队列去更新了。
直接在里面 std::sort() 复杂度会多个 \(log\)(虽然对于数据水的也能过),但是运用归并排序的思想就可以达到 \(O(nlogn)\) 的复杂度。
首先在外面把元素按照斜率 \(k\) 排序,然后开始 CDQ分治。
对于区间 \([l, r]\) ,把其中元素的编号按照与 \(mid\) 的大小进行分类,\(\leq mid\) 的分到左边,\(>mid\) 的分到右边,因为要用 \([l, mid]\) 中的点更新 \((mid, r]\),所以要先把这些点找出来(也可以理解成按编号归并排序的一部分,值得注意的是这样的分法不会破坏斜率分别在左区间和右区间的单调性,即这一操作(只包括按照 \(mid\) 分类)完成后左右两个区间中的斜率仍然是分别单调的)。
接着递归进 \([l, mid]\) ,保证左区间已经被处理过了,才能更新右区间的元素。
现在左区间的点和信息都被处理好了,并且 \(x\) 是单调的(已经被处理好了,详见后述),加上右区间的元素的斜率 \(k\) 是单调的(还没有被处理过),所以就可以把左区间的点加入单调队列,然后去更新右区间的元素。
但是现在 \((mid, r]\) 中的元素只有来自 \([l, mid]\) 的贡献,可能取不到最优解,所以为了保证正确性还要递归进 \((mid, r]\) 继续处理右区间。
最后不要忘了,要利用归并排序将 \([l ,r]\) 中 点的 \(x\) 变为单调的,这样才能保证前面操作的正确性。(可以理解为递归进一个区间后,这个区间内点的 \(x\) 就会被处理成单调的,可以进行后续的操作)
这就是 CDQ分治 的大致过程。
其实上面说了这么多,就是要让区间 \([l, r]\) 满足如下的关系:
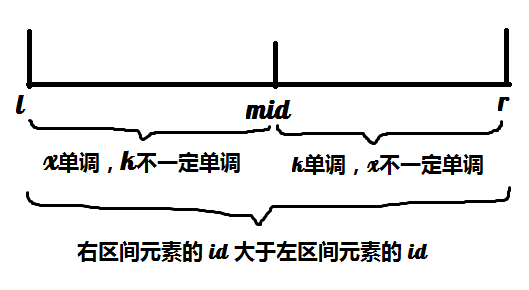
可以结合着图思考每一个操作分别有什么意义。
这样,斜率优化的基础知识就大概到这里了。(高级的我也不会)
接下来是一些题目(分析里仍然会有一些本篇文章的“原稿”,我也不打算改了)
1,[APIO2014]sequence 、 [USACO2008 Mar]土地购买
3,[CEOI2017]Building Bridges 、 [2018省队集训]序列