YZOJ P3791 餐馆

时间限制：2000MS      内存限制：524288KB

难度：\(6.0\)

• 题目描述

在一条东西向的街道上有 \(n\) 个餐馆，从西向东编号为 \(1\) 至 \(n\)，第 \(i\) 个餐馆和第 \(i+1\) 个餐馆的距离为 \(a_i\) 。

吃货小W喜欢到这条街道的餐馆里吃饭。现在，小W得到了 \(m\) 张餐票，每张餐票可以用于在街道上的任一餐馆里吃一餐。在第 \(i\) 个餐馆中，使用第 \(j\) 张餐票吃饭，可以获得的美味度为 \(b_{i,j}\) 。注意，每张餐票最多用一次，但在同一餐馆内可以使用任意多张餐票。

小W打算用完这 \(m\) 张餐票。他可以选择任一餐馆作为起点，每次吃饭时，可以选择一个餐馆，然后从当前位置（上次吃饭的地点，如果不存在则为起点）出发前往该餐馆并用任意一张未用过的餐票吃一餐，直到吃完 \(m\) 餐为止。小W希望最大化每次吃饭的美味度之和减去路上经过的总路程的值。

• 输入格式

输入第一行包含两个正整数 \(n,m\) 。

第二行包含 \(n-1\) 个正整数 \(a_1,a_2,\cdots,a_{n-1}\) 。

接下来 \(n\) 行，每行包含 \(m\) 个正整数，其中第 \(i\) 行第 \(j\) 个数为 \(b_{i,j}\) 。

• 输出格式

输出一行一个整数，表示所求的最大值。

• 样例输入

• 样例输出

• 样例说明

最优方案如下：以餐馆 \(1\) 为起点，在餐馆 \(1\) 使用第 \(1\) 张餐票、第 \(3\) 张餐票，然后前往餐馆 \(2\) 使用第 \(2\) 张餐票、第 \(4\) 张餐票。

• 数据规模与约定

对于所有数据，\(nm \leq 10^6\)，\(n \geq 2\)，\(a_i, b_{i, j} \leq 10^9\) 。

 

 

 

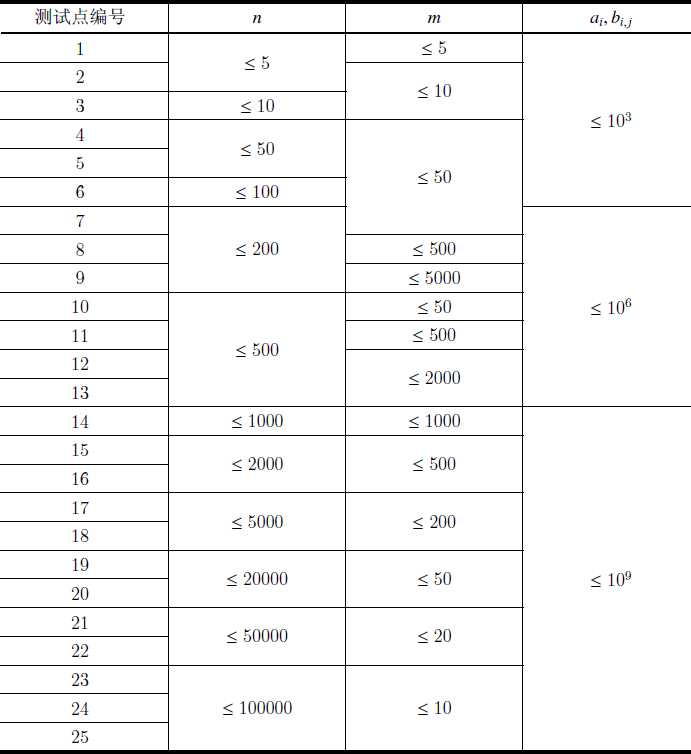
Source：ARC067 F – Yakiniku Restaurants，数据范围有改动（加强）

---

 

 

 

注意到（很显然爆零的我没有注意到）最优解肯定是在一段区间内，所以有

\(f_{l, r}=\sum\limits_{j=1}^m{\max\limits_{i=l}^r{b_{i, j}}} – \sum\limits_{i=l}^{r-1}a_i\)

直接 \(O(n^2)\) 枚举 \((l, r)\) ， RMQ \(O(m)\) 转移，暴力总复杂度 \(O(n^2m)\) 。

考虑优化，这里有两种办法：

法1，转换问题，对于每个 \((l, r)\) 区间寻找最优的 \(b_{i, j}\) 转化为 对于每个 \(b_{i, j}\) 寻找它能贡献的 \((l, r)\) 区间。对于一个 \(b_{i, j}\) ，很明显它能贡献的区间为 \((\)它左边第一个不比它小的数\(,\)它右边第一个比它大的数\()\) （既不重复也不漏算），这个过程可以用笛卡尔树维护（我也不知道为什么dalao们都用笛卡尔树（果然我不是dalao））两次单调栈维护，值得注意的是正反的两个单调栈有且只有一个必须加等号

发现可以把这一的贡献关系表示成 \(l\) 为横坐标 \(r\) 为纵坐标的坐标系 中的一些矩形，增加贡献区间就相当于矩形覆盖。即每次对于一个 \(l\) ，在所有包含 \(l\) 的贡献组成的平面中，找到权值最大的一个点（它的纵坐标相当于 \(r\)），用它来贡献 \(f_{l,}\) 。注意到这个过程可以使用扫描线（按 \(l\) 从小到大扫描）+线段树维护（扫到 \(l\) 时合法矩形中点的点权最大值），时间复杂度 \(O\left(nm \log \left(nm\right)\right)\) 。

 

 

 

 

---

法2，注意到若 \(f_{l, }\) 的最优贡献点在 \(k\) ，那么 \(f_{l+1, }\) 的最优贡献点一定不会在 \(k\) 之前，即决策单调性。证明自行感性理解（其实是我不会证）。所以分治一下即可，以 \(mid\) 为 \(l\) 时最优的 \(r\) 可能在 \([kl, kr]\) 中，时间复杂度 \(O\left(nm \log n\right)\) 。