YZOJ P2697 画圆
时间限制:1000MS 内存限制:131072KB
难度: \(5.1\)
-
题目描述
在初中数学课上,\(Alkri\) 学习了圆的相关知识,他对与圆有关的问题更加感兴趣了。
\(Alkri\) 想在平面直角坐标系的第一象限中依次画 \(n\) 个与两坐标轴均相切的圆,其中,第 \(1\) 个圆的半径为 \(r\),之后的每个圆都比上一个圆大,且与上一个圆相切,也就是说,对所有整数 \(2 \leq i \leq n\),第 \(i\) 个圆的半径大于第 \(i-1\) 个圆的半径且与第 \(i-1\)个圆相切。
例如当 \(n=3\) 时,三个圆 \(C_1, C_2, C_3\) 如下图所示(由于 \(C_3\) 比较大,未画完整):
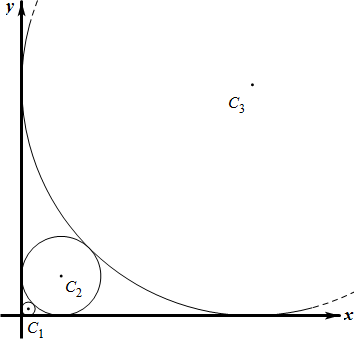
现在,\(Alkri\) 很好奇:第 \(n\) 个圆的半径 \(R\) 到底有多大?他知道 \(R\) 不一定是整数(真聪明!),并且可能非常大,所以只需要你保留 \(R\) 的整数部分(向下取整)的末尾 \(p\) 位数字即可。
-
输入格式
输入仅一行,包含三个整数 \(n\),\(r\),\(p\),意义如题目所述。
-
输出格式
输出仅一行一个整数,表示第 \(n\) 个圆的半径 \(R\) 的整数部分的末尾 \(p\) 位。注意当 \(R\) 的整数部分实际位数超过 \(p\) 时需要输满 \(p\) 位(即需要保留前导0),如果实际位数不满 \(p\) 位则不用补前导 0 。
-
输入样例
|
1 |
10 5 5 |
-
输出样例
|
1 |
08989 |
-
样例说明
第 \(10\) 个圆的半径整数部分为 \(38808989\),要求输出整数部分的末尾 \(5\) 位数,因此输出 \(08989\) 。注意保留前导 0 。
-
数据规模与约定
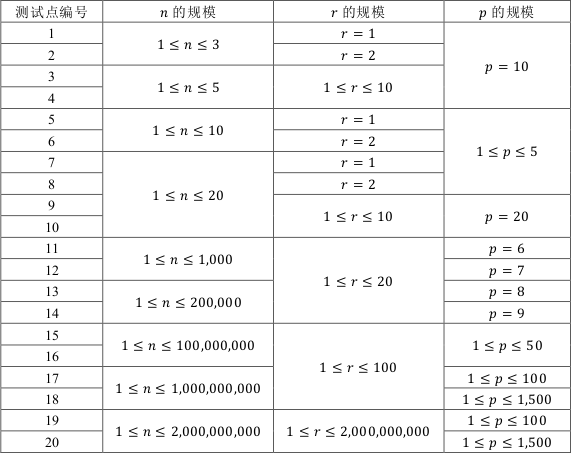
通过简单的数学计算可得下一个圆的半径是前一个圆的半径的 \(3+2\sqrt2\) 倍。(不要问为什么,题解说的
那么答案就是 \((3+2\sqrt2)^{n-1}r\) ,首先 \(50pts\) 就到手了。因为 \(n\) 很大的时候肯定会爆精度,所以无法开什么 long double 暴算。
高精度是肯定要写的,那么怎么写就是一个比较关键的问题。
可以新定义一个结构体表示 \(a+b\sqrt2\) ,其中 \(a, b\) 是两个高精度整数。这样就可以用整数表示出带根号的数了!这样,\((a+b\sqrt2)(c+d\sqrt2)=(ac+2bd)+(ad+bc)\sqrt2\) ,就是两个结构体相乘的方法了。
所以答案就是 \((3+2\sqrt2)^{n-1}r=Ar+B\sqrt2r=\cdots\cdots\) 。。。。。。好像没什么用?好像还是需要 \(\sqrt2\) 的近似值才能算???
这个时候就要想起奥数班sxb老师的教诲(好像当时数字也是这个来着的)
发现这个 \(\sqrt2\) 是真的很讨厌,就必须想办法把它弄掉。
注意到二项式定理。
\((a+b)^{n}=\sum\limits_{i=0}^{n} C_n^i a^{n-i} b^i\)
\((a-b)^{n}=\sum\limits_{i=0}^{n} \left([i\;\bmod\; 2\; =\; 0](C_n^i a^{n-i}b^i)+[i\; \bmod\; 2 \;=\; 1](-C_n^i a^{n-i}b^i)\right)\)
写成这样其实就非常清楚了,所以把它们相加的话
\((a+b)^n+(a-b)^n = 2\sum_{i=0}^{n} ([i\;\bmod\; 2\; =\; 0])(C_n^i a^{n-i}b^i)\)
在这里,若使 \((3+2\sqrt2)^{n-1}=A+B\sqrt2\) ,那么 \((3+2\sqrt2)^{n-1}+(3-2\sqrt2)^{n-1}=2A\) 。
所以答案就是 \((3+2\sqrt2)^{n-1}r=2Ar-(3-2\sqrt2)^{n-1}r=\cdots\cdots\) 。。。。。。好像没什么用?不!!有非常大的用处!!!!!!
因为 \(3-2\sqrt2 \approx 0.17 < 1\) ,所以可以试着计算一下 \((3-2\sqrt2)^{14} \approx 2 \times 10^{-11} < 10^{-10} < \frac{1}{r}\) ,也就意味着 \(n\) 足够大(其实也就 \(15\))时,\((3-2\sqrt2)^{n-1}r < 1\) ,所以答案就是 \(2Ar-1\) 。
这样 \(n\) 小的时候 long double 暴算一下,\(n\) 大的时候高精算一下就可以通过本题了!!!
(还要注意的是,保留小数位数那里前导 0 的判断要十分谨慎,我调了2d才调出来w
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 |
#include <cstdio> #include <cstdlib> #include <cstring> #include <climits> #include <cmath> int P; #define MAXDIG (P+(SETDIG<<1))/SETDIG #define SETDIG 3 #define SETDIGN 1000 struct _bnum { int num[1550],len; inline _bnum CutIDig() { //this->PrintNum(); if(len>MAXDIG) { for(register int i=MAXDIG;i<len;i++) num[i]=0; len=MAXDIG; } //this->PrintNum(); //printf("%d %d\n\n",len*SETDIG,(int)log10(num[0])); return *this; } _bnum(){memset(num,0,sizeof(num));len=0;} _bnum(const char str[]) { memset(num,0,sizeof(num));len=0; register int ls=strlen(str)-1; for(;ls-SETDIG>=0;ls-=SETDIG,len++) for(register int j=ls-SETDIG+1;j<=ls;j++) (num[len]*=10)+=(str[j]-'0'); for(register int j=0;j<=ls;j++) (num[len]*=10)+=(str[j]-'0'); len++; } _bnum(const int&n) { memset(num,0,sizeof(num));len=1; num[0]=n; while(num[len-1]>SETDIGN-1) num[len]=num[len-1]/SETDIGN,num[len-1]%=SETDIGN,len++; } _bnum operator = (const _bnum&ot) { len=ot.len; memcpy(&num,&ot.num,sizeof(num)); return *this; } _bnum operator += (const _bnum&ot) { register int flen=len; if(ot.len>flen) flen=ot.len; for(register int i=0;i<flen;i++) { num[i]+=ot.num[i]; if(num[i]>SETDIGN-1) num[i+1]++,num[i]-=SETDIGN; } if(num[flen]) flen++; len=flen; this->CutIDig(); return *this; } _bnum operator -= (const int&n) { num[0]-=n; for(register int i=0;i<len;i++) if(num[i]<0) num[i+1]-=(1-num[i]/SETDIGN),num[i]=(SETDIGN+num[i]%SETDIGN); else break; while(num[len-1]==0 && len>0) len--; if(len==0) len=1; return *this; } _bnum operator * (const _bnum&ot)const { _bnum ans; register int flen=this->len+ot.len; for(register int i=0;i<this->len;i++) for(register int j=0;j<ot.len;j++) ans.num[i+j]+=this->num[i]*ot.num[j]; for(register int i=0;i<flen;i++) ans.num[i+1]+=ans.num[i]/SETDIGN,ans.num[i]%=SETDIGN; while(ans.num[flen]) ans.num[flen+1]=ans.num[flen+1]/SETDIGN,ans.num[flen++]%=SETDIGN; while(ans.num[flen-1]==0) flen--; ans.len=flen; ans.CutIDig(); return ans; } inline void PrintNum() { static char outbuf[2048]; outbuf[0]=0; static char ots[8]; sprintf(ots,"%%0%dd",SETDIG); for(register int i=len-1;i>=0;i--) sprintf(outbuf+strlen(outbuf),ots,num[i]); register int ls=strlen(outbuf),si=ls-P; if(si<=0) for(si=0;outbuf[si]=='0';si++); for(register int i=si;i<ls;i++) printf("%c",outbuf[i]); printf("\n"); } }; struct _cs2 { _bnum a,b; _cs2(){a=b=0;} _cs2 operator *= (const _cs2&ot) { _cs2 ans; ans.a=this->a*ot.a,ans.a+=(_bnum)2*this->b*ot.b; ans.b=this->a*ot.b,ans.b+=this->b*ot.a; return (*this=ans); } }; inline _cs2 _pow(_cs2 M,int n) { _cs2 ans;ans.a=1,ans.b=0; while(n) { if(n&1) ans*=M; M*=M; n>>=1; } return ans; } int main() { int N,R;scanf("%d%d%d",&N,&R,&P); if(N<=15) { register long long ans=pow(3+2*sqrt(2),N-1)*R,pw10=pow(10,P); static char ots[8]; if(ans>=pw10) sprintf(ots,"%%0%dlld",P); else sprintf(ots,"%%lld"); printf(ots,ans%pw10); return 0; } _cs2 ans;ans.a=3,ans.b=2; (((_pow(ans,N-1).a*(_bnum)2)*(_bnum)R)-=1).PrintNum(); return 0; } |