YZOJ P3385 [校内训练20171201]笔名分配问题
时间限制:1000MS 内存限制:262144KB
难度:\(5.5\)
-
题目描述
班里有 \(n\) 个同学。老师为他们选了 \(n\) 个笔名。现在要把这些笔名分配给每一个同学, 每一个同学分配到一个笔名,每一个笔名必须分配给某个同学。现在定义笔名和真名之间的相关度是他们之间的最长公共前缀。设笔名为 \(a\),真名为 \(b\),则他们之间的相关度为 \(lcp(a,b)\)。那么我们就可以得到匹配的质量是每一个同学笔名和真名之间相关度的和。
对于两个字符串 \(a,b\)(从 \(1\) 开始标号),定义 \(a,b\) 的最长公共前缀 \(lcp(a,b)\) 为最大的非负整数 \(k\),使得 \(k\le |a|, k\le |b|\),且对所有 \(i=1,2,\ldots,k\),\(a_i = b_i\) 。
给出一种分配笔名的方案,使得匹配质量最大。
-
输入格式
第 \(1\) 行有 \(1\) 个整数 \(n\),表示班级中同学的数目。接下来 \(n\) 行,表示每一个同学的真名。最后 \(n\) 行是老师已经安排好的笔名。每行的名称仅由小写字母组成。
-
输出格式
将分配笔名的方案输出到文件中。第一行输出一个数,表示最大匹配质量。接下来 \(n\) 行,每行两个数 \(a,b\),表示把编号为 \(b\) 的笔名分配给编号为 \(a\) 的同学。同学和笔名均按输入顺序从 \(1\) 至 \(n\) 编号。若方案不唯一,任意输出一种即可。
-
样例输入
|
1 2 3 4 5 6 7 8 9 10 11 |
5 gennady galya boris bill toshik bilbo torin gendalf smaug galadriel |
-
样例输出
|
1 2 3 4 5 6 |
11 4 1 2 5 1 3 5 2 3 4 |
-
数据规模与约定
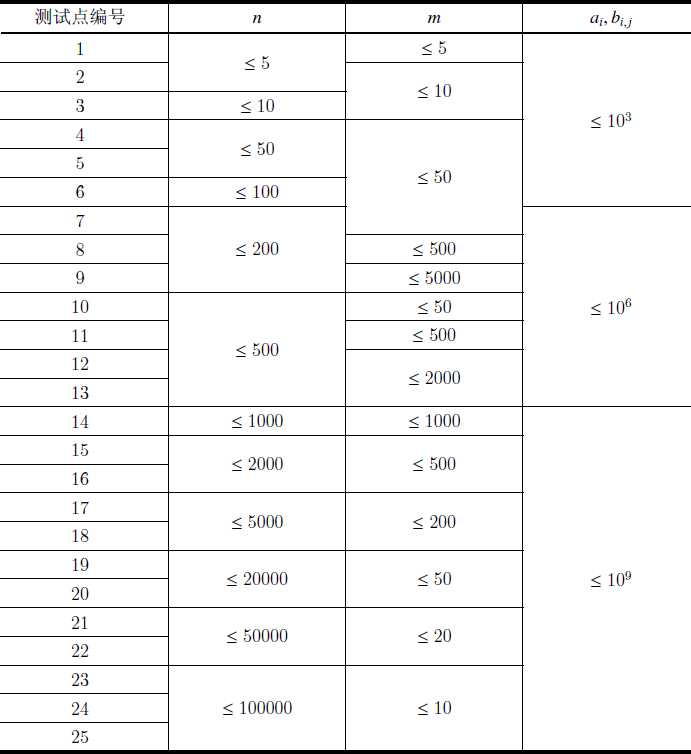
对于所有测试点,\(n \leq 100000\),输入串总长 \(\leq 800000\) 。